Table of Contents
The main purpose of clustering techniques is to partition a set of entities into different groups, called clusters. These groups may be consistent in terms of similarity of its members. All the representative-based clustering techniques use some form of representation for each cluster. Thus, every group has a member that represents it. The motivation to use such clustering techniques is the fact that, besides reducing the cost of the algorithm, the use of representatives makes the process easier to understand.
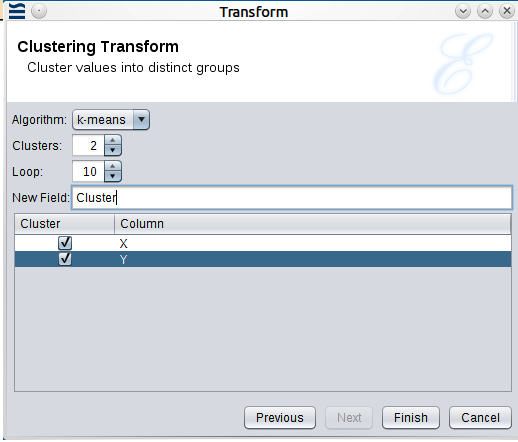
The transform currently supports k-means clustering. k-means clustering is a method of vector quantization, that is popular for cluster analysis in data mining. k-means clustering aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype of the cluster.
The data points for the cluster, must be in numeric format.
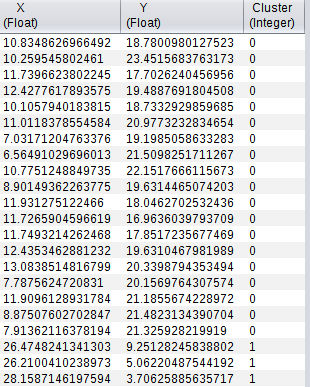
The following example shows the Clustering Transform and the converted results.
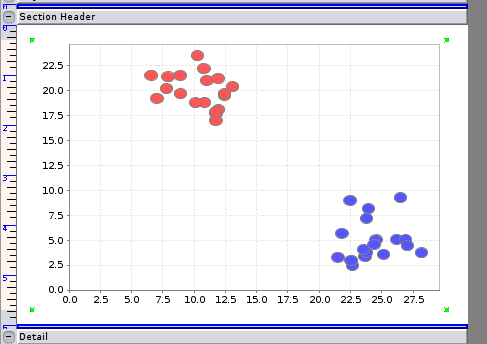
The following figure shows the output plotted as a bubble chart:The transform works with any number of numeric fields, but two fields are used for easy visualization of the results, in the above example.
k-means clustering is used in diverse fields such as market segmentation, computer vision, geostatistics, astronomy and agriculture.